柔性高分子缠结体系的动力学——高分子结构流变学的进展
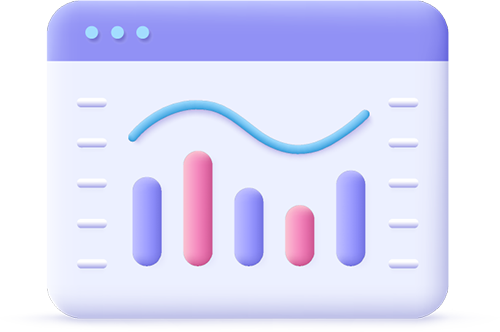
高分子缠结体系的动力学
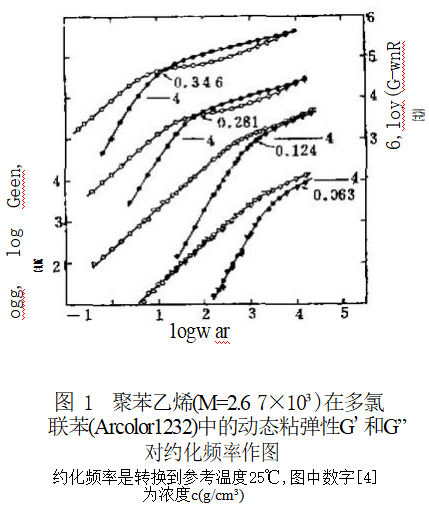
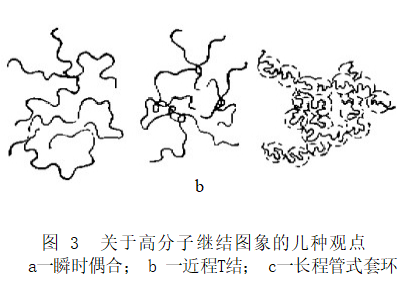
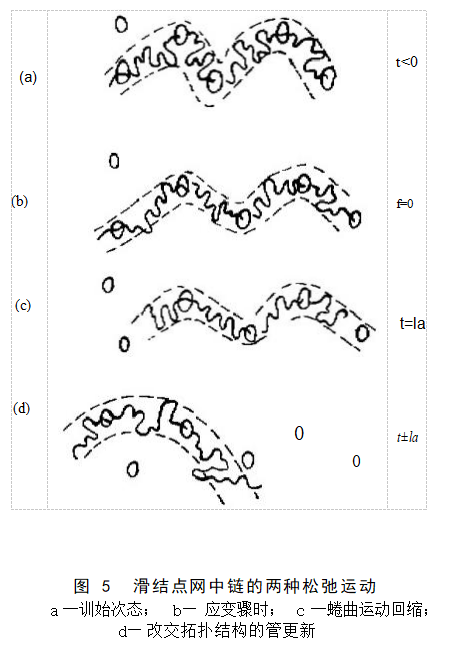
高分子熔体和浓溶液中的各种动力学行为是由长链分子的特异相互作用——缠结所决定的。这方面的进展是近年来高分子物理学中引人注目的方面。本文以缠结现象及其最新物理概念 的阐述出发介绍缠结体系动力学理论从网络模型向管式蠕动模型的进展和当前发展现状。强调了 在链段层次的相对不可透入性的管状概念是对新理论建立起关键作用的概念,有待进行更透彻的研究。 1 一、高分子浓体系的特征 随浓度提高,高分子开始互相接触,继而相互覆盖,这就进入了亚浓溶液的范围,这时空间各处的链段浓度还是不均匀的。此范围的分子链间相互作用可近似地用屏蔽效应来描述。但当浓度进一步提 高,高分子间穿越交叠使溶液成为各处链段 浓度大致均匀体系时,这一浓度称为缠结浓度,因为出现了新的分子间相互作用——缠结。这时高分子溶液就成为浓溶液。 线性粘弹性 缠结的发生可生动地用动 态粘弹性的实验来演示。图1是聚苯乙烯在 多氯联苯 (Aroclor1232) 中体系的实数模量 G'与虚数模量G”对频率作图。在浓度为 0.063g/c m³ 时曲线是Zimm 型的,当浓度提 高到接触浓度以上(0.124 g/cm⁴) 时曲线变 为Rouse 型,这是屏蔽效应的结果。在更高浓 度(0.281g/cm²) 下,发生缠结,G'与G”的 曲线交叉,并且虚模量出现一鞍形平缓区, 这反映了松弛时间谱要分为两组:高频部分是分子内自由度的松弛运动(Rouse 模式), 低频部分是缠结网松弛运动的贡献。 非线性粘弹性 在大形变和高形变速率 下,缠结网体系表现出特征的流变性,随速率增高发生粘度剪切变稀。这可归结为在流动 时分子必须要从一些缠结点的牵制下解脱, 而其重新生成需要时间,因此剪切速率越高, 缠结点越少,于是粘度降低。由于缠结网剪切时的弹性拉伸产生回缩力,高分子浓体系还表现出显著的法向应力效应。第一法向应 力函数N₁o=M°, 对熔体β=6~7,可见比粘度的分子量依赖性更强。可见少量高分子量部分的存在就可使缠结网显著加强。 综上所述,缠结的概念有可能对浓体系 各种流变性质提供统一的理解。但粗略的定 性解释不等于可靠的物理本质,缠结的概念 有待精确化、定量化,构成完整的数学模 型。 2 瞬时交联点与网络模型 在一个分子相互穿越交叠的缠结体系中,若把分子问的相互牵制视为分子链存在 瞬时交联点,那么浓体系就可视为类似橡胶 交联网,只是其中的交联点不是永久的化学 键,而是可生可灭的瞬时交联点,由此就可 以借用橡胶高弹性理论方法来处理其力学行为。 这个理论有以下5个基本假设: (1)高分子流体是三维交联网,交联点间距服从高斯分布,即构成一个三维高斯网络; (2)网络形变自由能来自构象熵的变化,忽略内能的变化; (3)网络整体构象熵变化是交联点间所有网链构象熵变化的加和; (4)交联点间网链的形变与弹性体整 体形变是仿射的; (5)瞬时网络引入的唯一新假设是:交联点处于产生和消失的过程中,它具有某种一定的寿命,由此引起网链的相应产生和消失。 Flory 很早就指出,网络理论中采用无 规行走网链的熵弹性的假定,即各网链的构 象互不妨碍,其实包含了一个幻影链(phan- tom chain) 的假设,即高分子链可以象 幻影一样相互透过,如图2所示,这是不可能的。 缠结概念的发展已有较长的历史, 早期的观念是局部打结的图象,如图3b 所示。 从力学性能估测缠结点间的分子量较大,缠 结点密度远少于分子链应有交叠点的密度, 从而推测存在一些相对牢固的绳结、成为缠 结点。但这种图象也遇到许多矛盾:按说柔性链才容易形成结环,但实验表明增加链的 刚性程度使缠结物性表现得更显著。 3 蠕动模型 管式蠕动模型的详细叙述有以下假设: 假设1:每个聚合物链在其它链构成的 笼中独立地运动,其运动限在一直径为α的 管中,如图4所示。由于该管是其它链的缠 结点的限制造成的,管式链也可等价于限制 在一系列滑结点中的链,这里滑结点的距离也是a。 假设2:真实链的运动用简化链 (pri- mitive chain) 表示,参见图4。简化链在 管的中轴,其弧长为 L, 它可视为步长为a 的自由连结链,即简化链的链段数为N=L/A。 假设3:简化链的链段在管中作布朗运 动,如同Rouse 链。 假设4:滑结点网中存在两种松弛运 动。 (1)当缠结网形变时,链从管中回 缩,这是熵弹性的作用,这种蠕动不改变网 的拓扑结构,它需要较短的松弛时间:ta~ M², 相 当 ;Rouse 链的松弛性质。 (2)简化链从各滑结点中脱出重新成 管,改变了缠结网的拓扑结构,称为管的更 新 。 如 图 5 所 示, t<0 时管处于平衡态 (a); 在 t=0 时加一形变,管也仿射地形变 (b); 经过ta, 分子蠕动,在管中回缩,脱出一 结点(c); 当达t=tg 时,布朗运动引起的扩散 使整个管子的拓扑结构改变(d); 假设5:应力张量为管中链段弹性力贡献的统计加和: 其中R; 为 i 链段未端的距矢量。 假设6:形变时活结点也仿射地变化位 置,这就建立了宏观与微观的关系: 形变中 Ri=F?R 其中F; '为相对形变梯度张量。应指出活结点的仿射性并不要求分子链的形状的仿射变 化,它可以滑动。 由扩散过程的计算,最后得到: 这样,从分子理论得到了原来唯象得到 的K-BKZ 类型的本构方程,这是对高分子 浓体系有最好实际描述能力的一类方程。